Finite Element Analysis in Python
In this note we go through the creation of a simple Python code that (1) defines element-wise stiffness matrix, (2) assembles the global stiffness matrix, and (3) solves the resulting system of equations by incorporating boundary and loading conditions.
Environment
TLDR: Use Colab.
There are two approaches to setting up your coding environment and get things going.
The easiest way is to use an online editor such as Google Colab. In Colab, click File-New notebook at the top left corner. Now you can start coding and also collaborate! The drawbacks of this approach are that (1) debugging is trickier (see this), (2) you have limited memory and CPU (since it is free!), (3) packages have to be installed on the fly, and obviously (4) you need to be online. But if you just started using Python, (1-3) are not your immediate concerns.
If you plan to work offline, then you will need to install a few things locally.
(1) Language: Please use Python 3 (Not Python 2 because syntax are different). For Windows users, I recommend Anaconda instead of the native Python since it comes with numerical computing packages (e.g., Numpy and sciPy) that you may encounter issues when installing on Windows.
(2) Development Environment: I recommend PyCharm and VScode. Both are free for students. Within the environment, you can code, test, and collaborate with others. It also allows you to manage Python packages more easily.
(3) Version Control (Optional): To collaborate with other people, you will need Git, which manages your files (e.g., compare differences between versions or restore to a previous version), and Github, which allows you to share your locally managed files with other people, so that you can simultaneous work on the same file and sync through github.
A Running Example
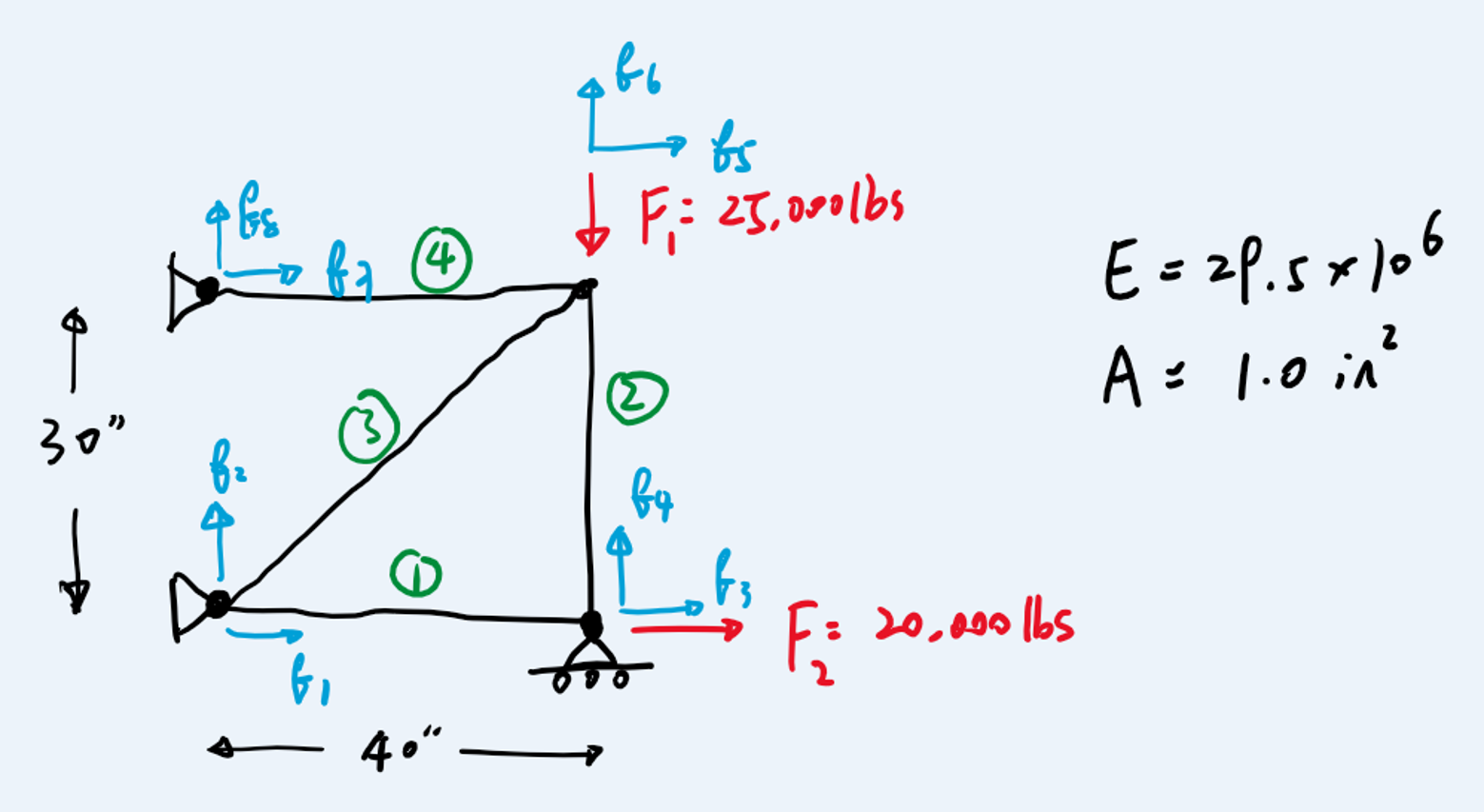
We use the following truss as a running example (see figure below). Here we have 4 nodes and 4 truss members (edges). We treat each truss member as an element. Each node has two degree of freedom, i.e., displacement in x and y directions. So the total degree of freedom without considering boundary conditions is 8, which are labeled as $q_1$ to $q_8$ in the figure. With the boundary conditions, $q_1$, $q_2$, $q_4$, $q_7$, and $q_8$ are fixed. Loadings are applied at $q_3$ and $q_6$.
A Truss Class
Here we define a class for a truss. We start with an initialization function that records the following parameters that define the truss: (1) nodes - the elements of this list are x- and y-coordinates of the nodes that define truss members; (2) edges - the elements of this list are pairs of node indices. Each pair defines a truss member; (3) fixed_dofs - this list specifies which degrees of freedom are fixed; (4) loads - this list specifies where loads are applied (5) E - Young’s modulus, assumed to be constant across the truss (6) A - cross section area, assumed to be constant across the truss
def __init__(self, nodes, edges, fixed_dofs, loads, E, A):
"""
:param nodes: A list of nodes with their coordinates in 2D
:param edges: Node connections: (0,2) node 0 and 2 are connected
:param fixed_dofs: A list of node constraints: (0,2,4) dof # 0, 2, 4 are fixed
:param loads: A list of point loads at nodes: (0,1000,0) dof # 1 has a point force of 1000
:param E: Young's modulus
:param A: Cross section area
"""
self.nodes = nodes
self.E = E
self.A = A
self.edges = edges
self.fixed_dofs = fixed_dofs
self.loads = loads
self.num_nodes = len(nodes)
self.dof = 2 * self.num_nodes
self.l = []
self.theta = []
self.k = []
self.dof_id = []
self.K = np.zeros((self.dof, self.dof))
For the running example, we use the following to create a truss. Notice that Python indexing starts with 0. So $q_1$ corresponds to the 0th element rather than the 1st.
nodes = np.array([[0., 0.], [40., 0.], [40., 30.], [0., 30.]])
edges = np.array([[0, 1], [1, 2], [0, 2], [2, 3]])
fixed_dofs = np.array([0, 1, 3, 6, 7])
loads = np.array([0, 0, 20000, 0, 0, -25000, 0, 0])
E = 29.5e6
A = 1
truss = Truss(nodes, edges, fixed_dofs, loads, E, A)
Element-wise Stiffness Matrix
Now we add a function to the truss class that computes the element-wise stiffness matrix based on (1) the orientation, (2) the cross section area, (3) the Young’s modulus, and (4) the length of the truss member.
# compute the element-wise stiffness matrix
def k_matrix(self, theta, A, E, l):
"""
:param theta: Orientation of the truss member
:param A: Area of the truss member
:param E: Young's modulus of the truss member
:param l: Length of the truss member
:return: Stiffness matrix
"""
c = np.cos(theta)
s = np.sin(theta)
return np.array([[c**2, c*s, -c**2, -c*s],
[c*s, s**2, -c*s, -s**2],
[-c**2, -c*s, c**2, c*s],
[-c*s, -s**2, c*s, s**2]])*A*E/l
Global Stiffness Matrix
Now we assemble the global stiffness matrix. To do so, we iterate over all truss members (edges).
For each member, we compute its length (l) and orientation (theta), which then allows us to compute
its element-wise stiffness by calling self.k_matrix(theta, self.A, self.E, l).
Lastly, we add the element-wise stiffness matrix to the global one.
The positioning of the element-wise matrix in the global one depends on the dof indices of that particular element
(which are [e[0] * 2, e[0] * 2 + 1, e[1] * 2, e[1] * 2 + 1]).
# assemble global stiffness matrix
def compute_stiffness(self):
for e in self.edges:
v = self.nodes[e[1]] - self.nodes[e[0]]
l = np.linalg.norm(v)
theta = np.arctan2(v[1], v[0])
self.l.append(l)
self.theta.append(theta)
self.k.append(self.k_matrix(theta, self.A, self.E, l))
self.dof_id.append([e[0] * 2, e[0] * 2 + 1, e[1] * 2, e[1] * 2 + 1])
self.K[np.ix_(self.dof_id[-1], self.dof_id[-1])] += self.k[-1]
Solve the FEA problem
We now define one last function for the truss class to solve the FEA problem.
In this function, we first call self.compute_stiffness() to prepare the global stiffness matrix.
Then we use the boundary conditions to find the sub matrix
corresponding to the actual degrees of freedom of the structure ($q_3$, $q_5$, $q_6$ in the running example).
Lastly, we solve the resulting linear system of equation to find the displacement of the actual degrees of freedom.
def solve(self):
self.compute_stiffness()
K = np.delete(np.delete(self.K, fixed_dofs, 0), fixed_dofs, 1)
loads = np.delete(self.loads, fixed_dofs)
return np.linalg.solve(K, loads)
Finding the internal forces on a truss element
Once we find the displacement, we can compute the forces on each truss member. To do this, we need to use the
element-wise stiffness matrix (k_element in the following code) and displacement (displacement_element).
The multiplication np.matmul(k_element, displacement_element) gives us the forces in the order of
(x-force of 1st node, y-force of 1st node, x-force of 2nd node, y-force of 2nd node).
displacement = np.zeros(truss.dof)
free_dofs = np.setdiff1d(np.arange(truss.dof), truss.fixed_dofs)
displacement[free_dofs] = truss.solve()
f_list = []
for i in range(len(truss.edge)):
e = truss.edge[i]
v = truss.nodes[e[1]] - truss.nodes[e[0]]
l = np.linalg.norm(v)
theta = np.arctan2(v[1], v[0])
k_element = truss.k_matrix(theta, A, E, l)
dof_element = [e[0] * 2, e[0] * 2 + 1, e[1] * 2, e[1] * 2 + 1]
displacement_element = displacement[dof_element]
f_element = np.matmul(k_element, displacement_element)
f_list.append(f_element)
Now you can call f_list[node_id] to get the forces for a specific node.
Complete Code for the Running Example
import numpy as np
# Class for 2D truss analysis
class Truss:
def __init__(self, nodes, edges, fixed_dofs, loads, E, A):
"""
:param nodes: A list of nodes with their coordinates in 2D
:param edge: Node connections: (0,2) node 0 and 2 are connected
:param fixed_dofs: A list of node constraints: (0,2,4) dof # 0, 2, 4 are fixed
:param loads: A list of point loads at nodes: (0,1000,0) dof # 1 has a point force of 1000
:param E: Young's modulus
:param A: Cross section area
"""
self.nodes = nodes
self.E = E
self.A = A
self.edges = edges
self.fixed_dofs = fixed_dofs
self.loads = loads
self.num_nodes = len(nodes)
self.dof = 2 * self.num_nodes
self.l = []
self.theta = []
self.k = []
self.dof_id = []
self.K = np.zeros((self.dof, self.dof))
# compute the element-wise stiffness matrix
def k_matrix(self, theta, A, E, l):
"""
:param theta: Orientation of the truss member
:param A: Area of the truss member
:param E: Young's modulus of the truss member
:param l: Length of the truss member
:return: Stiffness matrix
"""
c = np.cos(theta)
s = np.sin(theta)
return np.array([[c**2, c*s, -c**2, -c*s],
[c*s, s**2, -c*s, -s**2],
[-c**2, -c*s, c**2, c*s],
[-c*s, -s**2, c*s, s**2]])*A*E/l
# assemble global stiffness matrix
def compute_stiffness(self):
for e in self.edges:
v = self.nodes[e[1]] - self.nodes[e[0]]
l = np.linalg.norm(v)
theta = np.arctan2(v[1], v[0])
self.l.append(l)
self.theta.append(theta)
self.k.append(self.k_matrix(theta, self.A, self.E, l))
self.dof_id.append([e[0] * 2, e[0] * 2 + 1, e[1] * 2, e[1] * 2 + 1])
self.K[np.ix_(self.dof_id[-1], self.dof_id[-1])] += self.k[-1]
def solve(self):
self.compute_stiffness()
K = np.delete(np.delete(self.K, fixed_dofs, 0), fixed_dofs, 1)
loads = np.delete(self.loads, fixed_dofs)
return np.linalg.solve(K, loads)
nodes = np.array([[0., 0.], [40., 0.], [40., 30.], [0., 30.]])
edges = np.array([[0, 1], [1, 2], [0, 2], [2, 3]])
fixed_dofs = np.array([0, 1, 3, 6, 7])
loads = np.array([0, 0, 20000, 0, 0, -25000, 0, 0])
E = 29.5e6
A = 1
truss = Truss(nodes, edges, fixed_dofs, loads, E, A)
x = truss.solve()
displacement = np.zeros(truss.dof)
free_dofs = np.setdiff1d(np.arange(truss.dof), truss.fixed_dofs)
displacement[free_dofs] = x
f_list = []
for i in range(len(truss.edge)):
e = truss.edge[i]
v = truss.nodes[e[1]] - truss.nodes[e[0]]
l = np.linalg.norm(v)
theta = np.arctan2(v[1], v[0])
k_element = truss.k_matrix(theta, A, E, l)
dof_element = [e[0] * 2, e[0] * 2 + 1, e[1] * 2, e[1] * 2 + 1]
displacement_element = displacement[dof_element]
f_element = np.matmul(k_element, displacement_element)
f_list.append(f_element)