Report - NSF DEMS Project (2016-2017)

Participants: Ruijin Cang (PhD student), Houpu Yao (PhD student), Hechao Li (PhD student, graduated), Shaohua Chen (PhD student), Yaopengxiao Xu (PhD student), Yi Ren (Asst. Prof.), Yang Jiao (Asst. Prof.), Yongming Liu (Prof.)

Table of Contents

1. Executive Summary
2. Results and Findings
   1. Generative Model for Microstrutures and Topologies
   2. Structure-Property Prediction
   3. Modeling and quantification of microstructure evolution
   4. Efficient lattice particle simulation
3. Publications
4. Videos

Executive Summary

Through this project, we achieved the following goals and derived new research questions.

1. Microstructure patterns can be learned and used to generate new material samples. Material microstructures are usually represented as high-resolution images and are limited in quantity due to high acquisition costs through experiments. We developed generative models that learn the latent dimensions of microstructures, and create new microstructure samples that are morphologically and statistically similar to the limited samples. The developed model allowed us to bootstrap limited material samples to improve predictive structure-property models. See details here.

2. While deep networks outperform conventional models, they are not yet capable of capturing highly nonlinear structure-property mappings. The physics-based structure-property mapping often involves high computational cost, due to nonlinear constitutive models of material systems. We validated the hypothesis that deep learning architectures can outperform conventional nonlinear predictive models (such as Support Vector Regression) in predicting structure-property mappings. However, we found that even state-of-the-art deep convolutional neural networks cannot obtain the required prediction accuracy for material microstructure optimization.

3. Microstructure evolution of Ti64 during selective laser sintering is modeled and quantified. We developed a hybrid finite-element cellular-automaton model for microstructure evolution. This model is used for processing-structure mapping for Ti-6Al-4V (Ti64) alloy microstructures.

4. An efficient lattice particle simulation is developed for Ti64 fractual strength computation. A new atomic finite element method based on lattice particle is developed to replace an explicit solver to more efficiently compute Ti64 fracture strength. Nonlinear elasticity and plasticity constitutive models will be added to further refine the lattice particle model.

Results and Findings

The results and findings are summarized as follows.

Generative Model for Microstrutures and Topologies

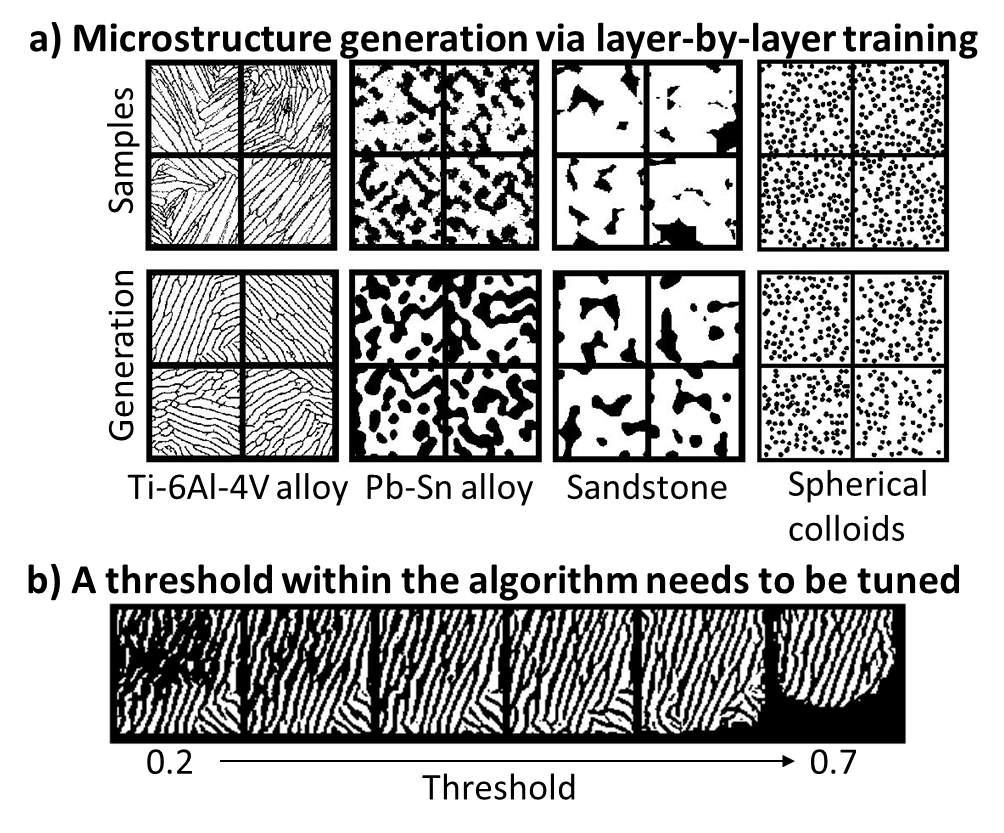
While state-of-the-art generative models have achieved photo-realistic image generation based on often enormous amount of training samples, it is well understood that these models will fail to learn meaningful local patterns (poor distribution matching) when only a small amount of data (in the scale of ten to a hundred) is available. The latter is usually the case in material design due to the high acquisition cost of microstructure samples. Therefore applying existing generative models to microstructures yielded generations with morphological difference from the samples, making these models inapplicable to material systems where properties are sensitive to morphological details. The PIs have partially addressed this challenge using a layer-by-layer learning mechanism through Restricted Boltzmann Machines (see Fig 1a), yet this model requires extensive calibration of the model parameters (see Fig 1b and the paper), as it only preserves morphologies within each layers, thus has limited control over the output morphology through a multilayer network.

Figure 1. (a) Samples and generations of Ti64, Pb-Sn, Sandstone and spherical colloids through layer-by-layer learning of a Convolutional Deep Belief Network. (b) The network requires material-dependent parameter tuning to reach good performance.

To this end, we investigate solutions inspired by style transfer (ST), a method that quantifies the style of an image as the variance-covariance matrices of the hidden-layer activations (denoted as the style vector) of a convolutional neural network (CNN) when the image passes through it, and optimizes new images to match their style vectors to the target (see Fig 2a for ST on material images). Nonetheless, ST is not generative, since the generation of each new image requires an optimization directly in the image space. Our model combines ST with a generative model: In each iteration of the training, we pass both the generated images and the samples through a pre-trained CNN (a very deep network) to calculate the discrepancy between their style vectors. This additional loss to be minimized regularizes the resultant generator to only generate images with styles consistent with the samples. It is worth noting that ST is also found to have better performance and less memory requirement than similar losses defined on correlation functions. Fig 2b compares the performance of generative models applied to several material systems with and without incorporating ST, with less than 100 samples in each case.

Figure 2. Generations through Style Transfer (ST), Variational Autoencoder (VAE), Generative Adversarial Network (GAN), and the proposed VAE+ST method.

The findings are summarized as follows:

• The layer-by-layer model (Convolutional Deep Belief Network) is effective at recovering microstructure details. Its parameters, however, require material-dependent tuning.
• The preliminary success with style transfer suggests that leveraging additional information in network training leads to better generations. This inspires the current investigation: Extending the idea of style transfer, we propose to regularize the generation through a physically meaningful loss. The loss will be calculated by measuring how well the generated microstructure matches the equilibrium state governed by the processing parameters.

Structure-Property Prediction

We investigated the utility of deep neural networks when applied to predict structure-property mappings. Two specific mappings are studied: The fracture strength of Ti64, and the Young’s modulus of sandstone. The fracture strength is computed by an explicit solver on a particle model of the Ti64 microstructure (see [the development of the model][Ti64model]). The Young’s modulus is computed via a Strong Contrast Expansion method, which expresses the elastic properties of a heterogeneous material in terms of individual phase properties and microstructural parameters involving the integration of correlation functions. Our findings are as follows.

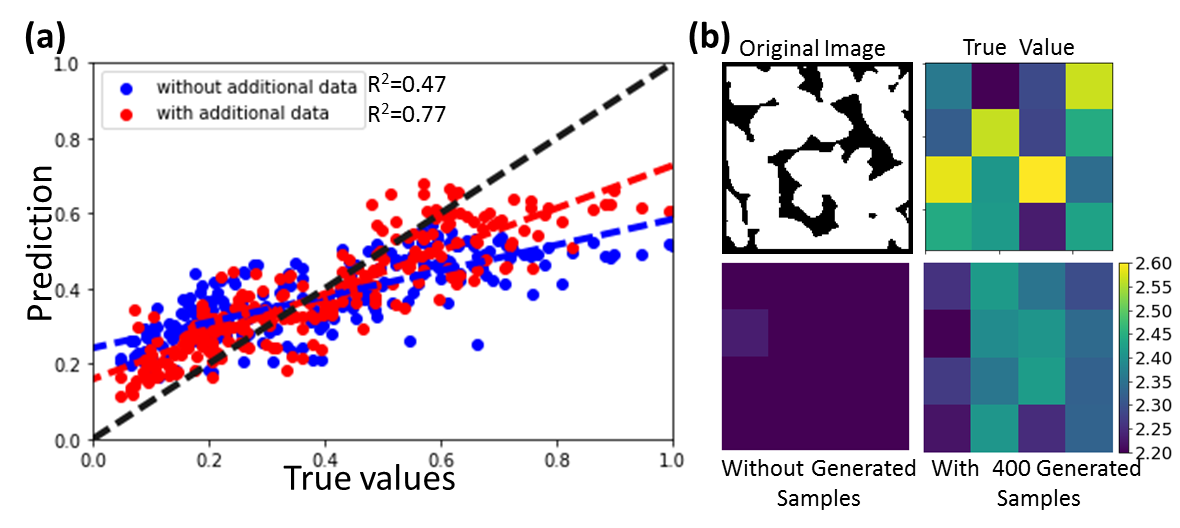
In the sandstone case, we used 40 images for training an initial residual network. We then used the developed generative model to create an additional 400 sandstone samples around those that have large prediction errors. The enriched dataset then leads to an improved predictive model as shown in Fig. 3a. To understand whether the network learns the correlation between structural patterns and the property, we scan a material sample and convert each small material patch to the void phase and evaluate the changes in Young’s modulus. We then compare the true changes with those derived from the prediction. Result shows that the improved model has better understanding of the local structure-property correlation, although there is still room for improvements (Fig. 3b).

Figure 3. (a) Comparison on the prediction performance of a residual network trained with 40 sandstone samples (blue) and with the additional 400 samples generated using the proposed VAE+ST model (red). (b) Sensitivity analysis of local structural patterns.

In the Ti64 case, we encountered difficulty in reaching plausible predictive performance for fracture strength, with extensive testing of network architectures. We should, however, note that the residual network still outperforms a standard benchmark (Support Vector Regression) with 1000 microstructure samples. This is because the residual network exploits the flexibility of an arbitrarily deep network while preventing the issue with local network convergence (which often causes poor prediction performance). It does so by shrinking a network layer to identity when the layer does not offer additional performance advantage. See Fig. 4.

Figure 4. Comparison on the prediction performance of a Support Vector Regression model (yellow), a VGG model (blue), and a residual network model (red).

The findings are summarized as follows:

• The generative model developed through this project can be used to enrich a small material dataset to improve the prediction performance of a resulting surrogate model.
• Deep networks achieve better performance in capturing structure-property mappings than standard surrogate models.
• Nonetheless, deep networks fail to predict highly-nonlinear mappings. This suggests that the incorporation of physics-based knowledge into the surrogate model is necessary.

Modeling and quantification of microstructure evolution of Ti-6Al-4V during selective laser sintering (SLS)

A hybrid finite-element cellular-automaton model for microstructure evolution in Ti64 during SLS has been developed and calibrated. The model incorporates the nonlinear variation of intrinsic material properties (i.e., specific heat, heat conductivity and material density) during SLS as well as temperature- and property-dependent heterogeneous nucleation and growth dynamics. It has been employed to investigate Ti64 microstructures associated with different processing conditions (laser power density, spot moving speed, etc). The alloy microstructures are subsequently quantified via spatial correlation functions to derive quantitative processing-structure relations.

Figure 5. (a) The temperature field on the surface of Ti64 resulting from a laser spot with radius 0.05mm and maximum powder 100W that moves at speed of 200mm/s along a zigzag path. (b) Distribution of vanadium concentration during SLS. (c) Distribution of alpha plate orientation in Ti64 microstructure during SLS. (d-e) Comparison of the simulated Ti64 microstructure (d) and an experimental system (e) obtained via the same SLS condition. (f) Scaled autocorrelation function f(r) associated with the alpha plate boundaries/ beta phase of the Ti64 microstructure obtained using different laser power densities and 3D simulated structures.

Efficient lattice particle simulation algorithms

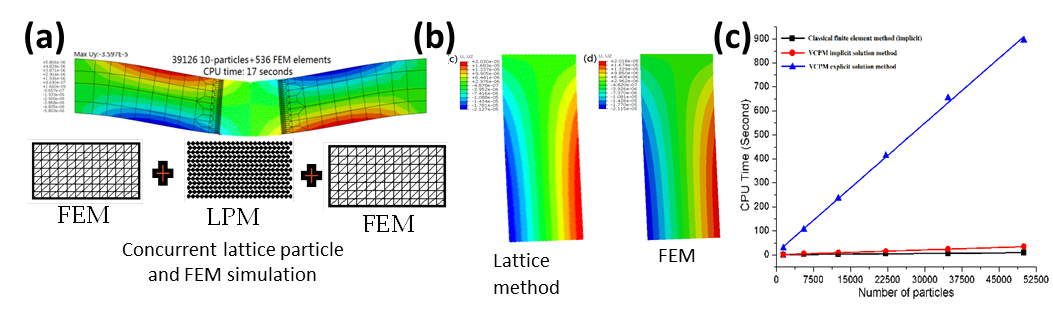
The commonly used explicit dynamic solution algorithm for lattice particle method is time consuming, especially for large scale simulations (e.g., many grains within 3D microstructure). A new atomic finite element method for the proposed lattice particle method is developed to address this issue. First, the energy minimization principle in AFEM will be applied to the developed non-local lattice formulation at the equilibrium condition during the quasi-static loading steps. The non-local stiffness matrix of elements will be constructed using the similar format in classical FEM. Connectivity in the non-local finite elements will be explored with respect to different crystal microstructures. Following this, the concurrent coupling between classical FEM and the lattice particle method will be developed. The concurrent coupling is achieved by a “faded layer” between the AFEM and FEM domain, where the non-locality gradually reduces from the AFEM domain to the FEM domain. Thus, a smooth transition between the non-local lattice method and FEM can be achieved without numerical artifacts at the boundaries (see Fig. 6(a) for a 2D example). Model verification will be performed for several benchmark problems (Fig. 6(b)). Significant improvement in computational efficiency is observed for the proposed atomic finite element formulation (Fig. 6(c)).

Figure 6. Efficient lattice particle simulation algorithms (a) coupled FEM and lattice particle simulation; (b) verification of simulation results with classical FEM method; (c) computation efficiency comparison of particle dynamics (blue), proposed method (red), and classical FEM (black) ***

Publications

• Cang, R., Xu, Y., Chen, S., Liu, Y., Jiao, Y., and Ren, Y. (2017). Microstructure Representation and Reconstruction of Heterogeneous Materials via Deep Belief Network for Computational Material Design. ASME Journal of Mechanical Design, 139(7), 071404.
• Cang, R., Vipradas, A., and Ren, Y. (2017). Scalable Microstructure Reconstruction with Multi-scale Pattern Preservation. In ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers.
• Cang, R., and Ren, Y. (2016). Deep Network-based Feature Extraction and Reconstruction of Complex Material Microstructures. In ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers.
• Chen, H., and Liu, Y. (2017). Micro/meso Scale Fracture Modeling Using A Novel Discrete Model. International Conference of Fracture, Greece, 2017.
• Xu, Y., and Jiao Y. (2017). Micro-structure and Superior Mechanical Properties of Hyperuniform Materials, 2017 TMS Annual Meeting, San Diego.

Videos