Design Competition 2 - Spring 2017

Paul Sharp - Monochrome 1963 Watercolour, The Mathematical Bridge Cambridge, United Kingdom. Image source: SULIS Fine Art
Problem Statement
Design a bridge using the following criteria:
-
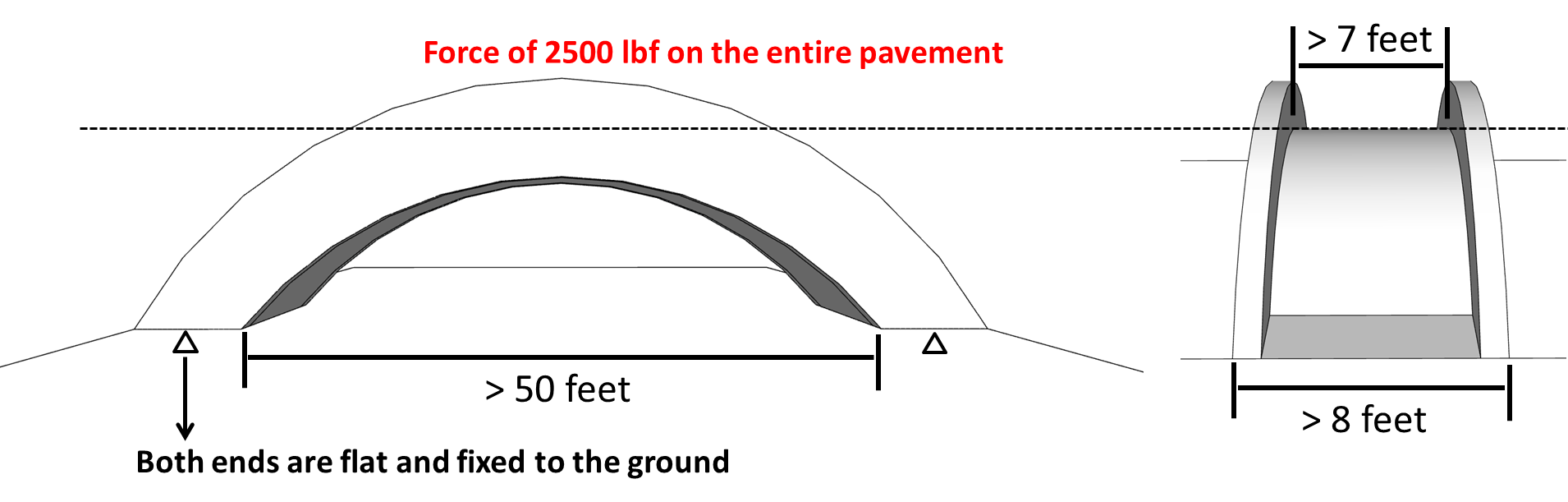
Dimensions: The bridge needs to be at least 50 feet (15.2 meters) long and at least 8 feet (2.4 meters) wide.
-
Material: For simplicity, the material of the entire bridge is assumed to be structural steel, with Young’s modulus $200~Gpa$, Poisson’s ratio $0.3$, and density of $7850 ~kg/m^3$ (use ANSYS default values).
-
Functionality: The bridge needs to be fully paved with the same material, so that pedestrians can easily pass. The pavement cannot have large positive/negative curvatures (See examples below) and should have a width of at least 7 feet (2.1 meters).

- Boundary conditions: The two ends of the bridge, which are apart from each other with a distance not smaller than 50 feet (15.2 meters), are fixed in x, y, and z directions to the flat ground. A downward force of 2500 lbf (11121 N) is applied to the entire pavement of the bridge. See figure below.
To apply the force, choose Force in ANSYS Mechanical, select all surfaces belonging to the pavement, and define the force by Components, where you can set the Y component to -11121 N.
-
Simulation: Use the coarse mesh for your model.
-
Design constraint: The total mass of the bridge needs to be below 55000 Pound (25000 Kg).
-
Design objective: The maximum deformation of the bridge in the load direction needs to be as small as possible.
Submission
Please submit the final design in ANSYS format (the .wbpj file should contain the geometry and the simulation) along with the associated folder in a zip file to yiren@asu.edu, with the file name “yourlastnameTeamNumber.zip”, e.g., “renTeam0.zip”. If the file is too large, please share it with me through Google Drive.
In the email, please also report the maximum deflection and the total mass values. The total mass can be found under the geometry tab in ANSYS Mechanical.
Make sure that the reported numbers are consistent with your model.